1-
History
of numbers
A long time ago
people used their fingers for counting (some still do!).
We begin here with the counting numbers (natural numbers,
positive integers)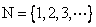 . Clearly this set is closed under the
operations of addition and multiplication but not under
subtraction. Thus it is natural to ask the following
question: . Clearly this set is closed under the
operations of addition and multiplication but not under
subtraction. Thus it is natural to ask the following
question:
Question 1
Can the above set be extended so that the extended set is
closed under the three previously mentioned operations?
The answer is clearly yes. Take the extended set to be the
set of integers
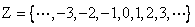 . The set of integers is not closed under
division though. So we ask a natural question: . The set of integers is not closed under
division though. So we ask a natural question:
Question 2
Can the set of integers be extended so that the extended
set is closed under the four basic operations?
The answer is yes. We denote the set of rational numbers
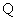 by by
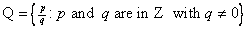 . .
However,
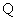 is not closed under the operation of taking
square roots. So here we go again and we ask: is not closed under the operation of taking
square roots. So here we go again and we ask:
Question 3
Can the set of integers be extended so that the extended
set is closed under the four basic operations as well as
the additional operation of taking square roots?
The answer as you might expect is yes. Take the set of
real numbers which is by definition the union of the sets
of rational an irrational numbers (the latter set is
nonempty since
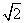 is not rational as one can see by a
standard contradiction argument; On the other hand, the
rational number system has certain gaps that were filled
by the mathematician Dedekind who gave use the real number
system. is not rational as one can see by a
standard contradiction argument; On the other hand, the
rational number system has certain gaps that were filled
by the mathematician Dedekind who gave use the real number
system.
Since the equation
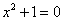 has no solutions in the set of real
numbers, we can ask: has no solutions in the set of real
numbers, we can ask:
Question 4
Can the set of real numbers be extended so that the
extended set is closed under the four basic operations,
taking square roots, and, in addition, so that equations
like
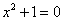 would have a solution in the extended set? would have a solution in the extended set?
A little comparison with a method of solving
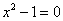 suggests
that the answer is yes after introducing the symbol suggests
that the answer is yes after introducing the symbol
 , and
here we witness the birth of the set of , and
here we witness the birth of the set of
Complex numbers
C
defined as
C={x+iy: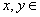 R}.
R}.
Notice that
C
clearly extends
R
and has the required properties.
Addition and subtraction of complex numbers are defined in
a natural way. Thus if
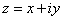 and and
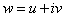 , then , then
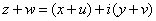 and and
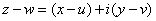 . We now define
multiplication of two complex numbers in such a way that
the existing laws (like the foil method) still hold which
explains why multiplication is defined as follows: . We now define
multiplication of two complex numbers in such a way that
the existing laws (like the foil method) still hold which
explains why multiplication is defined as follows:
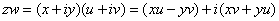 . .
Division is defined via conjugation (the conjugate of
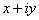 is
defined as is
defined as
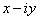 ). Thus if ). Thus if
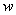 is a nonzero complex number, is a nonzero complex number,
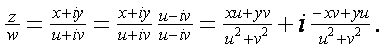
2- Triangle
Inequality
We now prove an important inequality called the
triangle inequality
For
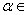 C
and C
and
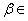 C,
we have C,
we have
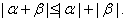
To see this, first note that
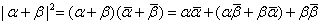
or
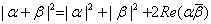
But
 So So
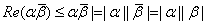 and therefore and therefore
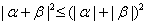 and
consequently and
consequently
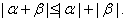
It is worth noting now that the
generalized triangle inequality
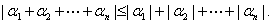
3- Limits
and Continuity
Definitions
As in real analysis, means for means for
 there is there is
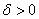 such that such that
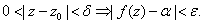
A function
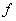 is
said to have a
limit
is
said to have a
limit
 at
at
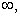 denoted by
denoted by
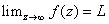 ,
if given ,
if given
 there exists a
large positive number there exists a
large positive number
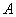 such that
such that
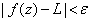 when
when
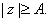 In addition,
In addition,
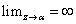 means
given an arbitrary means
given an arbitrary
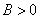 there exists a
there exists a
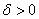 such that for
such that for
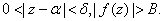
Definitions
A function
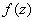 is said to be
continuous
at
is said to be
continuous
at
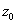 if
if
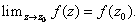
4-
Differentiable and holomorphic
functions
Definitions
A function
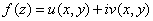 is differentiable
at is differentiable
at
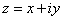 if the partial derivatives if the partial derivatives
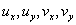 are continuous and
satisfy the Cauchy-Riemann equations are continuous and
satisfy the Cauchy-Riemann equations
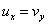 and and
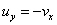 . The function . The function
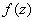 is differentiable in a region if it is
differentiable at each point
is differentiable in a region if it is
differentiable at each point
 in the region. in the region.
A function
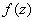 is analytic
(or
holomorphic)
at
is analytic
(or
holomorphic)
at
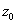 if
if
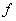 is differentiable in some disk
is differentiable in some disk
 . A function . A function
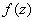 is analytic in a region if it is analytic at each point in
the region. A function
is analytic in a region if it is analytic at each point in
the region. A function
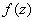 is called an entire
function
if it is analytic in the whole plane
C.
is called an entire
function
if it is analytic in the whole plane
C.
|

