1.
MEAN VALUE PROPERTY AND THE
MAXIMUM PRINCIPLE AND THEIR CONNECTION, SCHWARZ LEMMA
1.1
Mean
Value Property
Motivation.
If
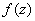 is an analytic function, then it can be represented as
a power series
is an analytic function, then it can be represented as
a power series
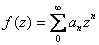 on a disk of convergence D(0,r). In addition, we
know by Cauchy’s Integral Formula that, in particular,
on a disk of convergence D(0,r). In addition, we
know by Cauchy’s Integral Formula that, in particular,
 or by parametrization
or by parametrization
 which states that the value of f at 0 is
the mean (average) value of f on a circle
centered at 0 with radius r. More
generally, it follows that if S is a closed disk
contained in an open set D where f is
holomorphic, the value of f at the center of
S is the mean of the values of f on the
circumference of S (considering the more general power
series
which states that the value of f at 0 is
the mean (average) value of f on a circle
centered at 0 with radius r. More
generally, it follows that if S is a closed disk
contained in an open set D where f is
holomorphic, the value of f at the center of
S is the mean of the values of f on the
circumference of S (considering the more general power
series
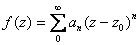 ). ).
Definition.
A
complex-valued function defined and continuous on an
open subset D of
C
is said to have the Mean Value Property (MVP) if
for each compact disk S contained in D, the value of
f at the center of S is the mean value of
f on the circumference of S.
Remark.
If f
has the MVP, then
 (where
(where
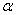 and
and
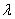 are complex constants) have the MVP.
are complex constants) have the MVP.
1.2
Maximum Modulus Property
Definition.
Let D
be an open subset of
C
and let
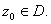 Let f be a real-valued function defined and
continuous on D. We say that f has a
relative maximum at
Let f be a real-valued function defined and
continuous on D. We say that f has a
relative maximum at
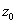 if
if
 such that
such that
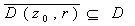 and and
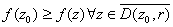 . .
Definition. .
Let D
be an open subset of
C
and let f be a complex-valued function defined
and continuous on D. We say that f has
the Maximum Modulus Property (MMP) on D if
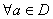 and and
 we have
we have
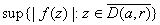 is
attained at a point of is
attained at a point of
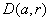 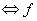 is
constant on is
constant on
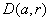 (I)
(I)
Equivalently (exercise), f has the MMP on D
if
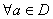 we have:
we have:
|f|
has a relative maximum at a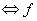 is
constant in a neighborhood of a
(II) is
constant in a neighborhood of a
(II)
1.3
Connection between MVP and MMP
Theorem
1.
Suppose
that f is defined, continuous, and has the MVP
on an open subset D of
C.
Then f has the MMP on D.
Proof.
We apply
(II). First, if f is constant in a neighbourhood
of
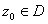 ,
then ,
then
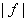 has a relative maximum at
has a relative maximum at
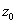 . Then there exists
. Then there exists
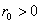 such
that such
that
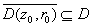 and and
 We need to show that f is constant on
We need to show that f is constant on
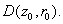 If
If
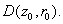 ,
then ,
then
 on on
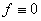 and in particular on
and in particular on
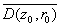 Suppose then that
Suppose then that
 .
Define a function g on D by .
Define a function g on D by

Note
that
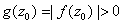 and
g has the MVP (since f does). Now
consider the function and
g has the MVP (since f does). Now
consider the function
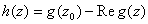 on D. Then h has the MVP on D.
Note that
on D. Then h has the MVP on D.
Note that and
and
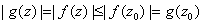 .
So .
So
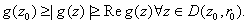 Thus
Thus
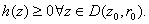 Let
Let
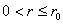 and
and
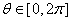 .
Since f has the MVP on D, we get .
Since f has the MVP on D, we get

But
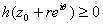 .
It follows that .
It follows that
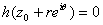 or or
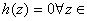
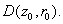
So
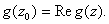 Now
Now
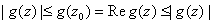 or or
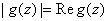 .
Thus .
Thus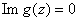 and therefore
and therefore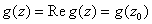 ; that is
; that is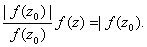 ,
Consequently, ,
Consequently,
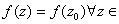 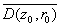 . .
Theorem
2.
Let D
be a bounded domain in
C
and let f be defined and continuous on
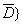 .
Suppose that f has the MVP on D and let .
Suppose that f has the MVP on D and let
 . .
If M
is attained at a point in D, then f is
constant on D (and hence on
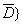 since f is continuous on D).
since f is continuous on D).
Proof.
Suppose
that M is attained at a point
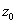 in D; that is,
in D; that is,
 for
for
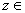 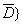 . .
Put
 .
Since .
Since
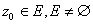 .
Moreover, if .
Moreover, if
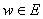 ,
then ,
then
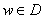 with
with and so for
and so for
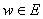 , ,
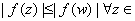 .
Thus .
Thus
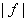 has a relative maximum at w. Since f has
the MVP on D, f has the MMP on D.
It follows that f must be a constant in a
neighbourhood V of w. Thus
has a relative maximum at w. Since f has
the MVP on D, f has the MMP on D.
It follows that f must be a constant in a
neighbourhood V of w. Thus
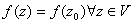 .
So .
So
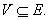 Therefore E is open in D. Since D
is connected, E=D. Consequently,
Therefore E is open in D. Since D
is connected, E=D. Consequently,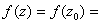 constant on D.
constant on D.
1.3
Maximum Principle
Theorem 3.
(Maximum Principle). Suppose
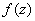 is a non-constant analytic function in an open subset
is a non-constant analytic function in an open subset
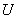 of
of
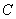 .
Then the function .
Then the function
 has no maximum in
has no maximum in
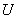 . .
Proof.
Suppose
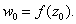 Then there is a disk
Then there is a disk
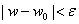 contained in the image of
contained in the image of
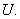 But in this disk there are points whose moduli are
But in this disk there are points whose moduli are
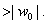 Consequently,
Consequently,
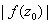 is not the maximum of
is not the maximum of

The Maximum Principle is sometimes
stated as:
Theorem 4.
(Another formulation of the Maximum Principle).
Suppose that
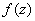 is analytic on a closed and bounded set
is analytic on a closed and bounded set
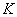 .
Then the maximum of .
Then the maximum of
 is attained on the boundary of
is attained on the boundary of
Proof.
Since
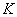 is a closed and bounded subset of
is a closed and bounded subset of
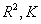 is compact. Thus
is compact. Thus
 attains its maximum on
attains its maximum on
 If
If
 is constant, there is nothing to prove. We can now
assume that
is constant, there is nothing to prove. We can now
assume that
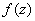 is not a constant function. Suppose, to get a
contradiction, that the maximum is attained at a point
inside
is not a constant function. Suppose, to get a
contradiction, that the maximum is attained at a point
inside
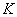 Then there is
Then there is
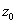 inside
inside
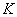 such that
such that
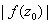 is maximum. Thus there is a disk
is maximum. Thus there is a disk
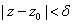 in
in
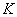 such that
such that
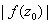 is the maximum among all the values
is the maximum among all the values
 , with in this disk. But this is only
possible if
, with in this disk. But this is only
possible if
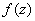 is constant. This is the desired contradiction.
is constant. This is the desired contradiction.
1.4
Minimum
Principle
Theorem 5.
(Minimum Principle)
Let f(z) be analytic inside and on a simple
closed curve C. If
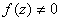 inside C, then |f(z)| assumes its minimum
value on C.
inside C, then |f(z)| assumes its minimum
value on C.
Proof.
Since f(z)
is analytic inside and on C and since
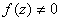 , it follows that
, it follows that
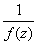 is analytic inside C. By the Maximum Principle
is analytic inside C. By the Maximum Principle
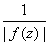 cannot assume its maximum inside C and so |f(z)|
cannot assume its minimum value inside C. Since
|f(z)| has a minimum, this minimum must be
attained on C.
cannot assume its maximum inside C and so |f(z)|
cannot assume its minimum value inside C. Since
|f(z)| has a minimum, this minimum must be
attained on C.
1.5
Schwarz
Lemma
Theorem 6.
(Schwarz Lemma). Suppose
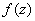 is analytic for
is analytic for
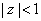 , ,
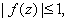 and
and
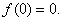 Then
Then
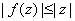 where equality holds only when
where equality holds only when
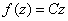 for some constant C whose absolute value is 1.
for some constant C whose absolute value is 1.
Proof.
It is natural to define the function
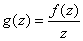 if z≠ 0 and f’(0) if z=0.
if z≠ 0 and f’(0) if z=0.
Since
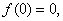
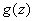 is analytic for
is analytic for
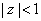 .
Let .
Let
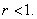 On the circle,
On the circle,
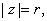 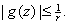 By the maximum Principle,
By the maximum Principle,
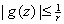 for
for
 Letting
Letting
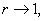
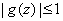 for all
for all
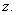
Suppose that equality holds; that is suppose that there
is a
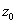 such that
such that
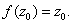 Then
Then
 Let
Let
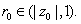 By the first part,
By the first part,
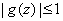 for all
for all
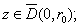 that is,
that is,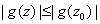 for all
for all
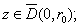 which means that the maximum is attained at
which means that the maximum is attained at
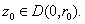 By the Maximum Principle
By the Maximum Principle
 must be constant; that is, there exists a constant C such that
must be constant; that is, there exists a constant C such that
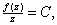 which means that
which means that
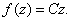 Moreover,
Moreover,
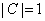 since
since
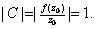 |

