1. CAUCHYíS
INEQUALITY, LIOUVILLEíS THEOREM, AND PARSEVALíS
IDENTITY
1.1
Cauchyís Inequality
Theorem 1.
(Cauchyís Inequality). Let
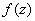 be analytic in a disk
be analytic in a disk
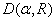 and let
and let
 be the circle
be the circle
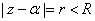 .
Suppose .
Suppose
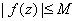 in
in
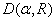 for some positive constant
for some positive constant
 . Then
. Then
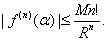
Proof.
By the previous corollary we get
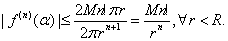
The result follows after letting
 . .
1.2
Liouvilleís Theorem
Theorem 2.
(Liouvilleís Theorem). A bounded entire function
must be constant.
Proof.
By the previous corollary for
 and for every
and for every
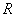 we can write
we can write
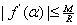 .
Let .
Let
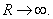 Then
Then
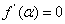 .
Since .
Since
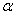 was arbitrary,
was arbitrary,
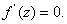 But then
But then
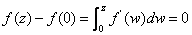 and thus
and thus
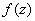 is constant. is constant.
1.3
Parsevalís Identity
Theorem 3.
(Parsevalís
Identity).
Let
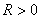 and for
and for
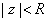 let
let
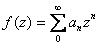 . .
Then for
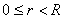 ,
we have ,
we have
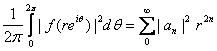 . .
Proof.
Consider
the partial sum
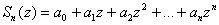
of the series
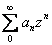 . .
Then
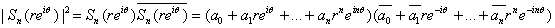
Multiplying out, integrating from 0 to
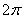 ,
and using ,
and using
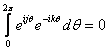 when
when
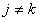 and
and
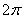 when j=k we get
when j=k we get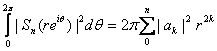
.
Since
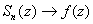 uniformly on @
uniformly on @
 and and
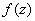 is bounded on is bounded on
 ,
it follows that ,
it follows that
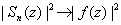 uniformly on
uniformly on
 .
Letting .
Letting
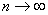 gives
Parsevalís identity. gives
Parsevalís identity.
|

