12.
APPLICATIONS TO THE FUNDAMENTAL THEOREM OF ALGEBRA AND
OTHERS
12.1
Fundamental Theorem of
Algebra
Theorem 1.
(Fundamental Theorem of Algebra). A non-constant
polynomial
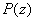 has at least one root. has at least one root.
Proof.
First note that
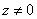 ,
for otherwise ,
for otherwise
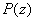 would reduce to a constant. Now
would reduce to a constant. Now
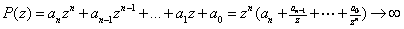 as
as
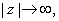 and hence there is a positive number
and hence there is a positive number
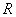 such that
such that
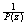 is bounded outside
is bounded outside
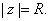 Moreover,
Moreover,
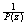 is also bounded on
is also bounded on
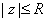 being continuous on this compact subset of
C and so
being continuous on this compact subset of
C and so
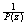 is bounded on
C. If is bounded on
C. If
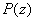 has no roots, then
has no roots, then
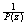 is also entire and so, by Liouville’s
Theorem, is also entire and so, by Liouville’s
Theorem,
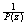 is constant and therefore is constant and therefore
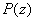 is constant. This contradiction
completes the proof of the theorem. is constant. This contradiction
completes the proof of the theorem.
12.2 Other Applications
We can now easily
prove a fascinating theorem about complex numbers.
Theorem 2.
Every non-constant complex polynomial of degree
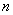 has exactly
has exactly
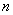 zeros. zeros.
Proof.
For every positive integer
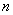 and all complex numbers and all complex numbers
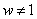 we know that we know that
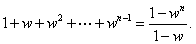
Thus for
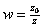 where
where
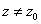 we get
we get

Multiplying by
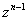 we get
we get
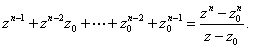
from which it
follows that
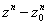 is divisible by
is divisible by
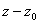 . .
Now, by the
Fundamental Theorem of Algebra, there is a value
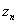 such that
such that
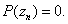 So
So
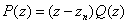 where
where
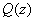 is a polynomial of degree
is a polynomial of degree
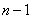 .
By induction if .
By induction if
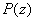 is a polynomial of degree is a polynomial of degree
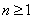 ,
then ,
then

where
 and
and
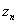 are constants. Consequently, every
non-constant complex polynomial of degree are constants. Consequently, every
non-constant complex polynomial of degree
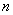 has exactly has exactly
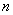 zeros. zeros.
Theorem 3.
Suppose that
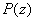 is a polynomial with real
coefficients. If is a polynomial with real
coefficients. If
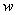 is a non-real zero of is a non-real zero of
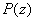 , then the conjugate of , then the conjugate of
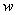 is also a zero of is also a zero of
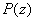 . .
Proof.
Suppose that
 is a polynomial with real coefficients. Since
is a polynomial with real coefficients. Since
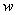 is a zero of is a zero of
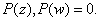 By conjugation,
By conjugation,
 Then
Then
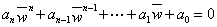 and consequently,
and consequently,
 is a zero of
is a zero of
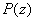 . . |

