14. SINGULARITIES AND WEIERSTRASS THEOREM
If
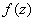 is analytic only in a punctured disk
is analytic only in a punctured disk
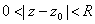 , then
, then
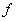 is said to have an isolated
singularity
at is said to have an isolated
singularity
at
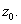 Let A denote the set of all isolated
singularities. We say that the isolated singularity
Let A denote the set of all isolated
singularities. We say that the isolated singularity
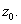 is an artificial (or removable)
singularity if f can be extended to is an artificial (or removable)
singularity if f can be extended to
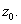 so that the resulting function
is holomorphic on so that the resulting function
is holomorphic on
 .
An isolated singularity of .
An isolated singularity of
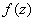 at at
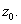 is called a pole
of is called a pole
of
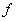 if if
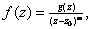 where
where
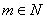 , ,
 is analytic in
is analytic in
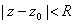 and
and
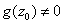 .
The integer .
The integer
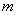 is said to be the order of the pole
and if
is said to be the order of the pole
and if
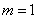 ,
then we say that ,
then we say that
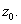 is a simple pole of is a simple pole of
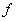 . .
We say that the
isolated singularity
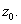 is an essential singularity if is an essential singularity if
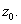 is neither an artificial singularity
nor a pole. is neither an artificial singularity
nor a pole.
A function
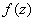 is called a meromorphic
function if is called a meromorphic
function if
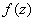 is analytic
for all values in
C except at points where poles
occur. is analytic
for all values in
C except at points where poles
occur.
Theorem.
An isolated singularity of
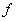 at at
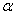 is a pole if and only if
is a pole if and only if
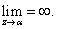
Proof ( )
This follows immediately from the definition of a pole. )
This follows immediately from the definition of a pole.
(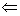 )
Let )
Let
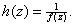 Then
Then
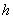 has an isolated singularity at
has an isolated singularity at
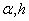 is not identically
is not identically
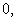 and
and
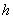 has a removable singularity at has a removable singularity at
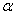 Then it is easy to show that there
exists a positive integer Then it is easy to show that there
exists a positive integer
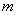 such that such that
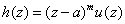 in a neighborhood of
in a neighborhood of
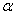 where where
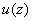 is analytic there with
is analytic there with
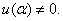 Thus
Thus
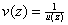 is analytic in a neighborhood of
is analytic in a neighborhood of
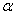 Now Now
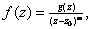 with
with
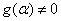 and the proof is complete. and the proof is complete.
We can now write down the following immediate-to-prove
but practical:
Corollary.
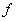 has a pole of order has a pole of order
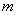 at at
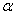 if and only if if and only if
 has
a zero of order has
a zero of order
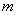 at at
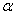
Examples.
1)
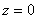 is an artificial singularity of
is an artificial singularity of
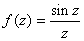 since since

2)
For
each integer n,
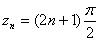 is
a simple pole of is
a simple pole of
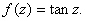
3)
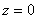 is an essential singularity of is an essential singularity of
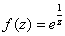 since
since
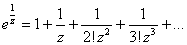
Weierstrass Theorem. Let
A be a singular subset of an open subset D
of C
and let f be holomorphic in D-A. If
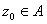 is
an essential singularity of f, then for every
r>0 with is
an essential singularity of f, then for every
r>0 with
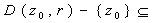 D-A we have
D-A we have
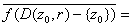 X. X.
Proof. The proof is by
contradiction. Assume that
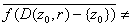 X.
Then there exists X.
Then there exists
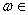 X
such that X
such that
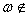  .
Then there exists .
Then there exists
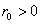 such
that such
that
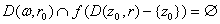 .
So .
So
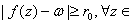 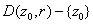 .
Thus the function .
Thus the function
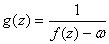 is holomorphic in
is holomorphic in
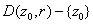 and
and
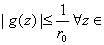 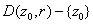 . That is, g is bounded in . That is, g is bounded in
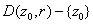 . By a previous proposition . By a previous proposition
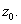 is an artificial (removable)
singularity of g. So we may regard g as a
holomorphic function on is an artificial (removable)
singularity of g. So we may regard g as a
holomorphic function on
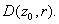 We now seek a contradiction in each
of the following two exclusive cases: We now seek a contradiction in each
of the following two exclusive cases:
Case 1.
 : There exists : There exists
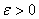 such
that such
that
 and therefore
and therefore
 such that
such that
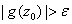
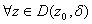 .
So .
So
 .
Therefore .
Therefore
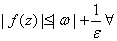
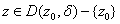 by the triangle inequality. That is, f is
bounded on
by the triangle inequality. That is, f is
bounded on
 .
Moreover, if .
Moreover, if
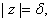 then
f is bounded being continuous there. As a
result, f is bounded on then
f is bounded being continuous there. As a
result, f is bounded on
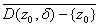 .
By a previous proposition, .
By a previous proposition,
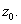 is a removable singularity of f
which is a contradiction. is a removable singularity of f
which is a contradiction.
Case 2.
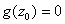 : That is : That is
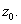 is a zero of g. Let m
denote the order of this zero. Thus there exists a
holomorphic function is a zero of g. Let m
denote the order of this zero. Thus there exists a
holomorphic function
 on on
 such that such that
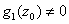 and and
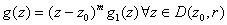 .
We have .
We have
  That is,
That is,
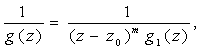 or or
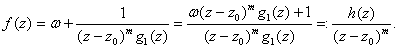 Notice that h is holomorphic on
Notice that h is holomorphic on
 and and
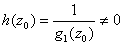 .
This means that .
This means that
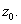 is a pole of f of order m
which is again a contradiction. is a pole of f of order m
which is again a contradiction.
|

