15. LAURENT SERIES
15.1
Analytic Functions in a Punctured Disk
Suppose that
 is an analytic function on a closed disk
is an analytic function on a closed disk
 .
Then .
Then

where
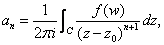
and
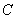 is the circle
is the circle
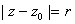 .
That is, an analytic function on .
That is, an analytic function on
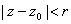 can be expressed there as a power series. But what about
those functions that are only analytic in the punctured
disk
can be expressed there as a power series. But what about
those functions that are only analytic in the punctured
disk
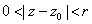 ?
It turns out, as we shall prove, that those functions
can be expressed in what is called Laurent series that
has some resemblance to power series: ?
It turns out, as we shall prove, that those functions
can be expressed in what is called Laurent series that
has some resemblance to power series:
Suppose then that
 is analytic in the punctured disk is analytic in the punctured disk
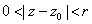 and has a pole of order and has a pole of order
 at
at
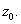 We then recall that there is an analytic function
We then recall that there is an analytic function
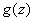 on
on
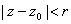 with with
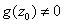 and such that
and such that
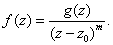
Let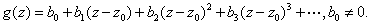 Then Then
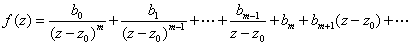
15.2
Principal and
Analytic Parts and Connection with Power Series
The sum of the terms involving
negative powers of
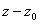 is a polynomial in powers of
is a polynomial in powers of
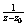 of degree
of degree
 , denoted by , denoted by
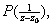 is called the principal part
of
is called the principal part
of
 at at
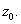 The other part is called the analytic part of
The other part is called the analytic part of
 at at
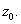 It
is standard to write It
is standard to write
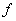 then as: then as:
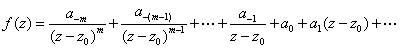
which is the Laurent series
of
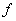 at at
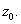
In short, we can write
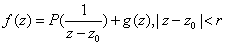
where
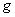 is analytic on is analytic on
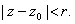
Suppose now that
 is an analytic function on a domain is an analytic function on a domain
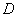 except at poles except at poles
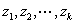 in in
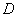 of orders of orders
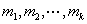 respectively. By repeated application
of the above procedure we immediately see the following: respectively. By repeated application
of the above procedure we immediately see the following:
Theorem 1.
. If
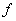 is an analytic function on a domain is an analytic function on a domain
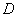 except at poles except at poles
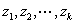 in in
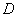 of orders of orders
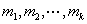 respectively, then respectively, then

where
 , ,
 are polynomials in are polynomials in
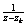 of degrees of degrees
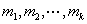 respectively and respectively and
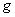 is analytic on is analytic on
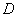 |

