RESIDUE THEORY
1.1
Cauchy’s Residue Theorem
We now state a theorem of practical importance called the
Cauchy Residue Theorem which allows us to compute
easily many integrals some of which can only be evaluated
using this theorem.
Theorem 1.
(Cauchy Residue Theorem). Suppose that
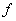is an analytic function on a simply-connected domain
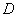except for a finite number of poles
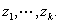Suppose that
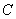is a piecewise smooth positively-oriented simple (does not
intersect itself) closed curve not passing through
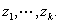Then
 ,
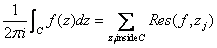where the sum is
over all the poles
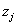of
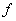that are inside
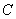
Proof.
By a previous theorem,
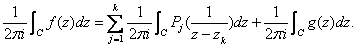
By Cauchy’s
Theorem,
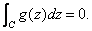 Moreover,
since
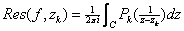
1.2
Jordan’s Lemma
In some cases we use the following:
Lemma 1.
(Jordan’s lemma). If
represents the curve
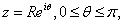
then
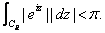
Proof.
On
,
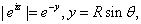and
Thus
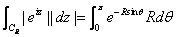
In the last
integral let
 ,
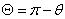then using
we ge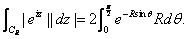t,
 But
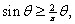for
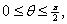from which the result follows.
As an application of Jordan’s lemma we consider the
following
Example. Show that
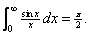
Method :
Since
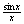is an even function, it suffices to show that
Let
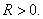Consider the integral
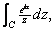where
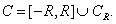However, since the singularity
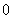is on the contour of integration, we consider instead the
integral
In this case,
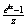 has
a removable singularity
Thus the function
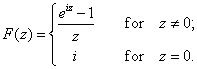
is entire and
is a closed contour in
.
Then by Cauchy’s Theorem we have
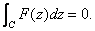
Then
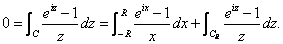
So
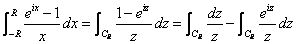
Equating
imaginary parts we get
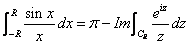
So
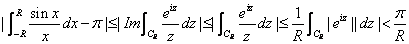
by using
Jordan’s lemma.
Finally, letting
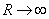establishes the result.
Method :
Let
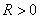be large and
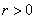be small. Now let
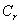represent the curve
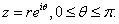
Consider the
integral
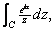where
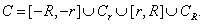Note that the function
has no singularities inside
.
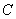Thus
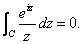
So
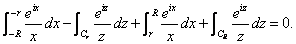
Letting
in the first integral we get
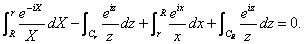
Combining we get
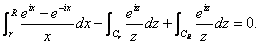
or
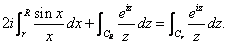
Moreover, near
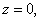we have the expansion
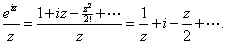
Hence
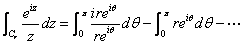
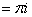 +terms
that tend to
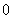as
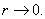
Furthermore, using Jordan’s lemma, we get
Finally, letting
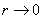and
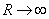establishes the result. |
