|
Definitions
A subset U of C
is said to be open
if
for each u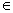 U there is a disk D(u,r)
such that D(u,r) U there is a disk D(u,r)
such that D(u,r) 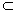 U. U.
A
neighborhood of a point x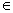 X X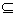 C
is any open set U C
is any open set U
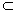 C
such that x C
such that x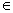 U . U .
A subset
F of
C
is said to be closed if its complement is open in
C.
A point
s is said to be a limit point
(or
accumulation point)
of a
subset S of
C
if each neighborhood of s contains at least one
point of S other than s.
Example.
The origin is an accumulation point of
C
and
C-{0}.
Theorem. F
is closed if and only if F contains all of its
limits points.
The following theorems are easy to prove:
Theorem.
Let 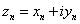 and
z=x+iy.
Then and
z=x+iy.
Then
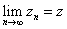 if and only if if and only if
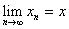 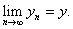
Theorem. 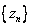 is
Cauchy if and only if is
Cauchy if and only if
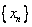 and and
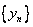 are Cauchy. are Cauchy.
Using this theorem, since
R
is complete
(every
Cauchy sequence in
R
converges to a point of
R),
it follows that
C
is complete.
Moreover,
C
is connected since the only clopen (closed and open)
subsets of
C
are the empty set
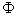 and
C. and
C.
Definitions.
A subset D of
C
is said to be connected if D is not
the union of two nonempty sets A and B such that
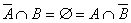 . .
A subset D of
C
is called a domain
if
D is open and connected.
A subset D of
C
is said to be convex if the line segment joining
any two points in D lies in D.
We state the following two properties:
Theorem.
Suppose that D is a subset of
C
such that every two points of D can be joined by a
polygon in D, then D is connected.
Theorem.
If D is a domain, then every two points of D
can be joined by a polygon in D.
Definitions.
a) A collection of open sets is an open cover of a
set X if X is contained in the union of
these open sets.
A
subset K of
C
is said to be compact
if
from each open cover
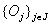 of K, one can extract a finite
subcover of K. of K, one can extract a finite
subcover of K.
Definition.
A sequence of complex numbers
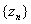 is said to have a limit z
if is said to have a limit z
if 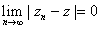 . .
 The following theorem is easy to prove: The following theorem is easy to prove:
Theorem.
Let 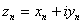 and and
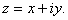 Then Then
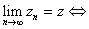
 and and
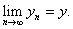
Definition.
A sequence of complex numbers
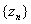 is said to be a Cauchy sequence
if is said to be a Cauchy sequence
if
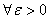 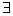 N N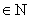 such that such that
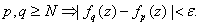
The following theorem is also easy to prove:
Theorem.
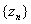 is a Cauchy sequence is a Cauchy sequence
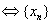 and and
 are Cauchy sequences. are Cauchy sequences.
Since
R
is complete (every Cauchy sequence in
R
converges), it follows from the preceding theorem that
C
is complete.
Definitions.
a) Let 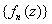 be a sequence of functions defined for
each be a sequence of functions defined for
each 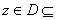 C. C.
We say that 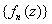 converges
to
f(z) if converges
to
f(z) if
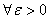 and for each z and for each z
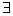 N N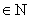 (which depends on (which depends on
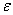 and z) such that and z) such that
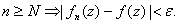
b) We say that
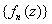 converges uniformly to f(z)
on D if converges uniformly to f(z)
on D if
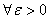 and for each z and for each z
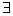 N N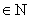 (which depends only on (which depends only on
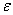 ) such that ) such that
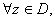 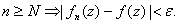
Clearly uniform convergence implies convergence
but the converse is not true.
The following theorem extends from real variables:
Theorem (Cauchy Criterion for uniform convergence of
sequences) 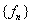 converges
uniformly to f on converges
uniformly to f on
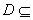 C C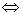 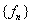 is Cauchy. is Cauchy.
Proof.
(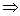 ) Given ) Given
 , ,
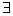 N N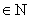 such that such that
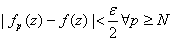 and and
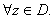
Now 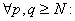 
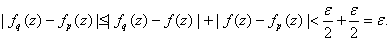
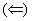 Given Given
 , ,
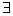 N N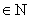 such that such that
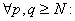 
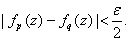
Fix z. Then
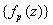 is a Cauchy sequence in
C
which is complete. Thus is a Cauchy sequence in
C
which is complete. Thus
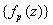 converges to converges to
 say. say.
Fixing p and letting q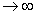 we get we get
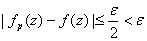  . .
For series of functions we have the
following criterion:
Theorem (Cauchy
Criterion for uniform convergence of series).
Consider
the sequence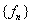 defined on a set defined on a set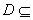 C.
Then C.
Then
 converges uniformly on D converges uniformly on D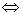 given given
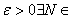 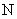 such that such that

Proof.
(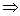 ) Consider the sequence of partial sums
with general term ) Consider the sequence of partial sums
with general term
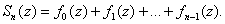 Since Since
 converges uniformly on D, converges uniformly on D,
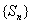 converges uniformly on D. By
Cauchy Criterion for uniform convergence of sequences,
given converges uniformly on D. By
Cauchy Criterion for uniform convergence of sequences,
given 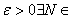 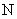 such that such that
 That is, That is,
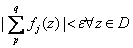 . .
( ) Using the hypothesis we can write ) Using the hypothesis we can write
 Again by Cauchy Criterion for uniform
convergence of sequences Again by Cauchy Criterion for uniform
convergence of sequences
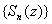 converges uniformly on D and
consequently converges uniformly on D and
consequently  converges uniformly on D. converges uniformly on D.
Example.
Let
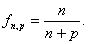
For a fixed n,
 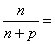 1. Now 1. Now
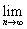  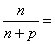 1. 1.
On the other
hand, for a fixed p,
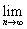 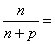 0. Now 0. Now
 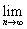 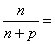 0. 0.
This wonít
happen with uniform convergence as the following theorem
shows:
Theorem.
Let a be a limit point of a
subset D of
C.
Suppose that
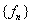 converges uniformly to f on
D and that converges uniformly to f on
D and that
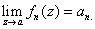 Then Then
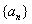 converges and converges and
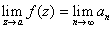 ; that is, ; that is,
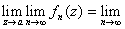 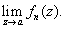
Proof.
The proof
is left as an exercise.
Theorem.
Suppose that
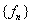 converges
uniformly to f on D and converges
uniformly to f on D and
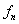 is continuous on D. Then f
is continuous on D. is continuous on D. Then f
is continuous on D.
Proof.
Fix
 It is enough to show that f is
continuous at It is enough to show that f is
continuous at 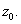 Let Let
 . Since . Since
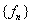 converges uniformly to f on
D, converges uniformly to f on
D,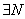 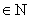 such that such that
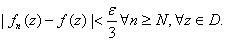
 In particular, for n In particular, for n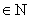 , ,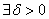 such that such that
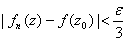 when when
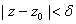 and and

Consequently,
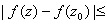 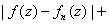 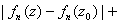 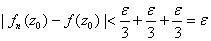
when
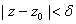 . .
The
following is another useful criterion for uniform
convergence of sequences:
Theorem
(Weierstrass Criterion for uniform convergence of
sequences).
Suppose
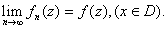 Put Put
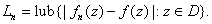 Then Then
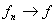 uniformly on D uniformly on D
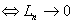 as as
Proof.
Follows
easily from the definition of uniform convergence.
Following
is the Weierstrass corresponding criterion for series
which is frequently quite
useful in
verifying uniform convergence:
Theorem (Weierstrass Criterion for
uniform convergence of series).
Suppose
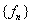 is a sequence of functions defined on
D such that is a sequence of functions defined on
D such that
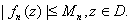
Then
 converges converges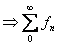 converges uniformly on D. converges uniformly on D.
Proof.
If
 converges, then, for arbitrary converges, then, for arbitrary
 , and for , and for
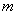 and n large enough: and n large enough:
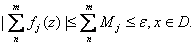 So So
 converges uniformly on D by
Cauchy Criterion for uniform convergence of series. converges uniformly on D by
Cauchy Criterion for uniform convergence of series.
Example.
Let
 The series The series
 converges uniformly on [-a,a]
because converges uniformly on [-a,a]
because
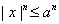 which
is the nth term of a convergent geometric
series. which
is the nth term of a convergent geometric
series.
We turn
now to the connection between uniform convergence and
integration.
We begin
wth the following theorem whose proof is left as an
exercise:
Theorem.
Suppose
that 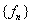 is a sequence of integrable
functions on [a,b] which is a sequence of integrable
functions on [a,b] which
converges
uniformly to f on [a,b]. Then f is
integrable and
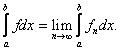
Following
is an important corollary:
Corollary.
Suppose
that 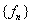 is a sequence of integrable
functions on [a,b] and is a sequence of integrable
functions on [a,b] and
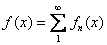 uniformly on [a,b]. Then uniformly on [a,b]. Then
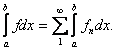
(term-by-term integration)
Proof
of Corollary.
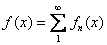 uniformly on [a,b] implies that
the sequence of partial sums { uniformly on [a,b] implies that
the sequence of partial sums {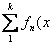 )} converges uniformly on [a,b].
Thus )} converges uniformly on [a,b].
Thus
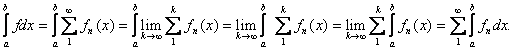
As an
application we consider the following problem which shows
the power of uniform
convergence as well as the care that we must take in
similar situations.
Problem.
Consider the
sequence of functions with general term :
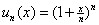 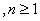 and and
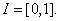
1) Show that
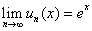 for every for every
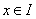
2) With
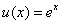 for for
 prove that prove that
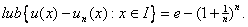
3) Deduce
that the sequence of functions with general term
 converges uniformly to converges uniformly to
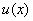 on on
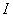 , ,
4) Deduce
that the sequence of functions with general term
 converges uniformly to converges uniformly to
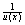 on on
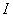 , ,
5) Deduce
the value of 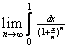
Solution:
1)
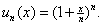 So ln So ln
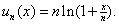 Using LíHopitalís Rule we get Using LíHopitalís Rule we get
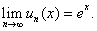
2) Consider
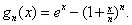
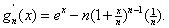
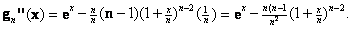
In general, and with an induction proof,
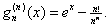
Now
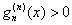 and so and so
 is increasing and is increasing and
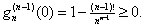
Since
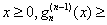 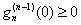 and so and so
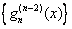 is increasing. So is increasing. So
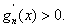
It follows
that
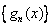 is increasing. Thus is increasing. Thus

Therefore
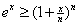 or or
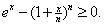
Thus
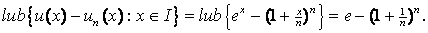
3)
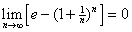 using 1). using 1).
By
Weierstrass Criterion for uniform convergence of sequences,
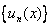
converges
uniformly to
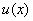 on on

4) Use 3)
and  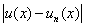 since since
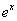 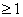 on on
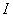 and and
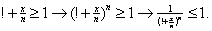
5)
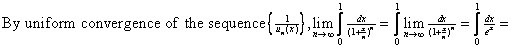
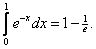 |

