1.
Rouche's Theorem with Applications
Rouche's Theorem.
Let f and g
be holomorphic functions in a domain D in
C
containing the closed disk
 . If . If
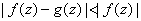 for for
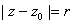 , then f and
g have the same number of zeros in , then f and
g have the same number of zeros in
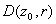 (note that the
hypothesis implies that f and g have no
zeros on the boundary of (note that the
hypothesis implies that f and g have no
zeros on the boundary of
 ). ).
For applications
the following variant of Rouche's Theorem is useful:
A variant of
Rouche's Theorem.
Let f and
h be holomorphic functions in a domain D in
C
containing the closed disk
 . If . If
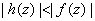 for for
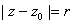 , then f and
f+h have the same number of zeros in , then f and
f+h have the same number of zeros in
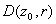
Example.
Show that the equation
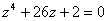
has exactly three distinct
solutions in
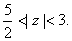
First, we apply Rouche's
Theorem on
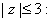
Let
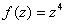 and and
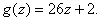
When
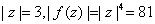 while
while
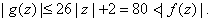
By Rouche's Theorem,
 and and
 have the same number of zeros in have the same number of zeros in
 That is, That is,
 has 4 zeros
in has 4 zeros
in
 . .
Next, we apply Rouche's
Theorem on
Let
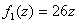 and and
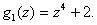
When
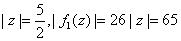 while
while
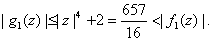
By Rouche's Theorem,
 and and
 have the same number of zeros
in have the same number of zeros
in
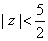 . That is, . That is,
 has one zero in has one zero in
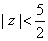 . .
Now we show that previously mentioned zeros lie on
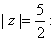
If
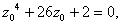 then
then
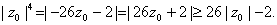 On On
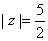 , this inequality is impossible. , this inequality is impossible.
Combining we see that
 has 3 zeros in has 3 zeros in
 To show that To show that
these zeros are distinct (i.e, that each zero in
 is
simple), suppose is
simple), suppose
 and and
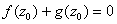 . Then . Then 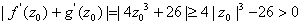
or
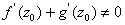 implying implying
that
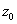 is a simple zero. is a simple zero. |

