|
Definition. A power series in z
is a
series of the form

where 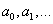 are complex constants. are complex constants.
The
operations of addition and subtraction of power series are
defined in a natural
way.
For multiplication we use
Cauchy’s Product.
We
define the product of
 and and
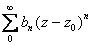 as the power series as the power series
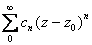 , where , where
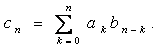
Theorem 1.
Suppose there exists some
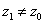 such that such that
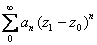 converges. Then for each z such
that converges. Then for each z such
that  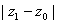 , the series , the series
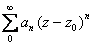 converges absolutely. converges absolutely.
Proof.
Let
r be a real number such that
 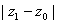 . Since . Since
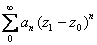 converges, converges,
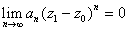 .
Thus, { .
Thus, { }is bounded. So there exists a constant
M>0 such that }is bounded. So there exists a constant
M>0 such that
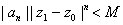 for all n. for all n.
Thus
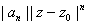 = =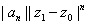 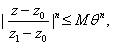 where where
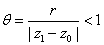 and so the series and so the series
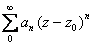 converges absolutely by the comparison
test with a convergent geometric series. converges absolutely by the comparison
test with a convergent geometric series.
Theorem 2. A
power series 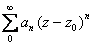 must satisfy one of the following must satisfy one of the following
1)
The series converges for
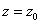 only. only.
2)
The series converges for all z.
3)
There exists an R>0 such that the series converges
for 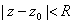 and diverges for and diverges for
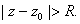
We
call the radius of convergence of the power series
the
extended nonnegative number R (Note that in the
first case we can take R=0 and in the second
R=∞).
Proof.
Without loss of generality assume that
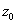 =0. Assuming that 1) and 2) do
not hold, it is enough to show that 3) does. Then the
series converges at some value =0. Assuming that 1) and 2) do
not hold, it is enough to show that 3) does. Then the
series converges at some value
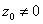 and diverges at some other value and diverges at some other value
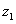 . Let S denote the set of all
numbers µ such that the series converges for . Let S denote the set of all
numbers µ such that the series converges for
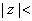 µ; S is nonempty by using Theorem 1.
Moreover, S contains no numbers larger than µ; S is nonempty by using Theorem 1.
Moreover, S contains no numbers larger than
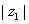 and so S is bounded from above.
By Real Analysis, S must have a least upper bound
which we call R. That R has the remaining
properties of 3) follows from Theorem
1. and so S is bounded from above.
By Real Analysis, S must have a least upper bound
which we call R. That R has the remaining
properties of 3) follows from Theorem
1.
Definitions.
Let
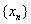 be a sequence in
R.
The limit superior of be a sequence in
R.
The limit superior of
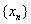 , denoted by , denoted by
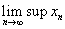 ,
is
the extended real number defined by ,
is
the extended real number defined by
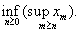 The limit inferior
of The limit inferior
of
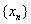 , denoted by , denoted by
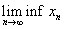 , is the extended real number
defined by , is the extended real number
defined by
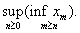
Theorem (Cauchy-Hadamard Rule).
R=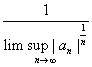
(with the convention that
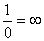 and and
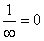 ). ).
To
prove the Cauchy-Hadamard Rule, we first state and
prove the following
Lemma (Cauchy’s Root Test,
1821).
Let 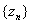 be a sequence in
C.
Then be a sequence in
C.
Then
a)
If 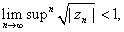 then then
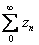 converges. converges.
b)
If 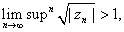 then then
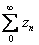 diverges. diverges.
Proof.
a)
Choose  such that such that
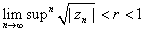 . Then, in particular, . Then, in particular,
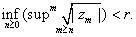 So there exists an integer So there exists an integer such that such that
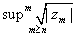 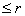 for otherwise the previous step is
contradicted. Thus for otherwise the previous step is
contradicted. Thus
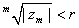 or or
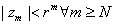 . Since r<1, . Since r<1,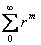 converges and so converges and so
 converges. It follows that converges. It follows that
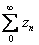 converges absolutely and hence
converges. converges absolutely and hence
converges.
b)
Suppose now that
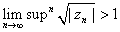 . Then . Then
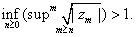 So for every So for every
 . In particular, . In particular,
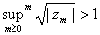 . Thus there exists an integer . Thus there exists an integer
 such that such that
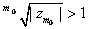 for otherwise the previous step is
contradicted. Again since for every for otherwise the previous step is
contradicted. Again since for every
 we have we have
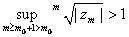 . Therefore there exists an integer . Therefore there exists an integer
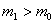 such that such that
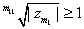 . Proceeding like this one can show
that there exists a subsequence . Proceeding like this one can show
that there exists a subsequence
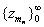 of the sequence of the sequence
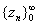 such that such that
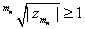 (i.e, (i.e,
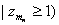 and so and so
 and consequently and consequently
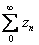 diverges. diverges.
Before proving the Cauchy-Hadamard Rule, let us
mention the corresponding:
d’Alembert Ratio Test
(1768). Let
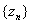 be a sequence in
C
with be a sequence in
C
with  . Then . Then
a)
If 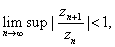 then then
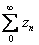 converges. converges.
b)
If 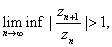 then then
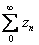 diverges. diverges.
whose proof follows by putting
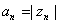 in the following inequality (proof left
as an exercise) in the following inequality (proof left
as an exercise)
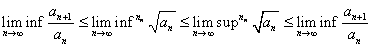
and
applying the root test.
Proof of the Cauchy-Hadamard Rule.
Let
 . Then . Then
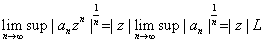 . .
By
the root test, if |z|L<1, then
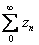 converges while if |z|L>1, then converges while if |z|L>1, then
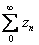 diverges. That is, diverges. That is,
if
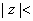 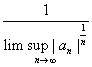 , then , then
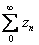 converges and converges and
if
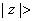 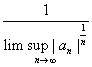 , then , then
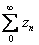 diverges. diverges.
Consequently R=
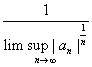 . .
Remark 1.
Note
that R is not necessarily
 as we shall see next: as we shall see next:
It
is enough to show that
  can happen. Indeed, let can happen. Indeed, let
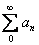 denote the series where denote the series where
 if n is even and if n is even and
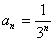 if n is odd. if n is odd.
Since 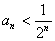 , the nth term of a convergent
(geometric) series, , the nth term of a convergent
(geometric) series,
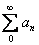 converges. converges.
Now
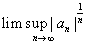 = =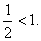 So So
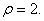 But, considering n odd, But, considering n odd,
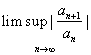 = =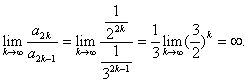
Consequently,
 =0<2= =0<2=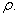
Remark 2.
If
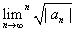 and and
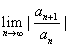 exist, then they must be equal (and as
a result R= exist, then they must be equal (and as
a result R= ): ):
Let
c=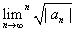 and d= and d=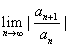 and without loss of generality assume
that c<d and get a contradiction. Choose and without loss of generality assume
that c<d and get a contradiction. Choose
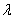 such that such that
 and let and let
 = =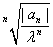 and consider the series and consider the series
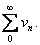
On
the one hand, 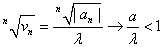 and the series and the series
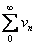 is convergent while, on the other hand, is convergent while, on the other hand,
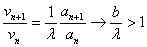 and the series and the series
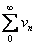 is divergent. is divergent.
Remark 3.
In
general, we have
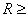 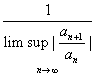 : :
Let
L= . Then . Then
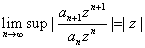 L. L.
By
the ratio test, when |z|L<1,
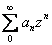 converges. That is, converges. That is,
When
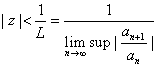 , ,
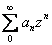 converges. Consequently, converges. Consequently,
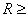  . . |

