1-
Curves, Arcs, and Contours, and a definition of
integration
A curve is given by the parametric equations x=x(t),
y=y(t) where x(t) and y(t) are
real-valued function on a closed interval [a,b].
An arc (or differentiable path) is a continuously
differentiable curve. A complex-valued function f(z)
is said to be continuous on an arc C if f[x(t)+iy(t)]
is continuous on [a,b] and in this case we define
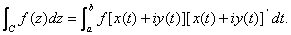
Under this definition almost all the rules of real
integrals carry over to complex ones of which we mention,
for instance, the following:
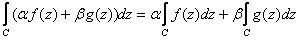 ,
where f(z) and g(z) are continuous on an arc
C and ,
where f(z) and g(z) are continuous on an arc
C and
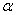 and
and
 are complex constants (exercise 2).
are complex constants (exercise 2).
However, using an alternative equivalent definition in the
next section makes it easier to carry on with other
complex integral properties.
Example. Let
 .
Let C be the circle centered at the origin of
radius R. We parametrize C as .
Let C be the circle centered at the origin of
radius R. We parametrize C as 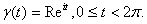 Then
Then
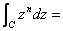 
Consequently, if , ,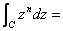
 . .
If
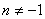 , ,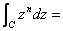 0 since n is an integer.
0 since n is an integer.
A collection of n arcs is said to form a contour
T if the end point of the arc C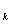 coincides with the initial point of
coincides with the initial point of
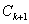 for
for
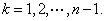 In this case, we define
In this case, we define
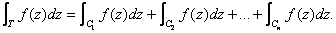
We now state and prove the Fundamental Theorem of Calculus
for complex functions:
2-
Theorem
Let
F(z)
be an analytic function with continuous derivative f(z).
Let T be a contour with initial point
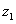 and terminal point
and terminal point
 .
Then .
Then
 . .
Proof. Without loss of generality, it is enough to show that
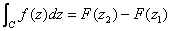
for an arc C with initial point
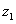 and terminal point
and terminal point
 . .
We use the chain rule together with the Fundamental
Theorem of Calculus for real functions:
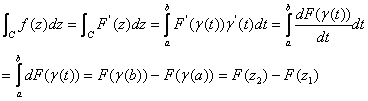
A simple curve is a curve that does not intersect
itself. A domain is said to be simply connected if
the interior of every simple closed curve in the domain is
contained in that domain.
3 -
An
equivalent definition of integration that is best suited
to prove
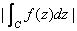  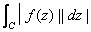
As in real analysis,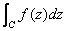 can be obtained as a limit of sums of the form
can be obtained as a limit of sums of the form
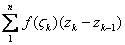 ,
where ,
where
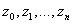 are points taken in succession along the curve C
are points taken in succession along the curve C
and
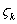 is on C between
is on C between
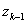 and
and
 .
This formulation makes it obvious, that the integral is,
to a large extent, independent of the parametric
representation of the curve C, and also leads to
an important inequality whenever .
This formulation makes it obvious, that the integral is,
to a large extent, independent of the parametric
representation of the curve C, and also leads to
an important inequality whenever

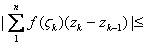 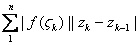 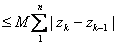
Since the straight line segment is the shortest distance
between two points
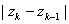 does not exceed the length of the part of the arc C
joining
does not exceed the length of the part of the arc C
joining
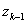 and
and
 .
Thus if L denotes the length of C, .
Thus if L denotes the length of C,
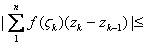 ML.
Taking limits, we get ML.
Taking limits, we get 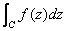
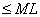 . . |

