|
Definition.
Let z=x+iy. Then the analytic function w=f(z)=u(x,y)+iv(x,y)
defines a transformation between the xy-plane
and the uv-plane. If the transformation is such
that the angle between two intersecting curves
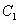 and
and
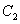 at
at
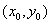 equals the angle between the corresponding curves
equals the angle between the corresponding curves
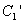 and
and
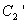 at
at
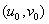 and the sense of the angles are also preserved, then the
transformation is called conformal at
and the sense of the angles are also preserved, then the
transformation is called conformal at
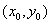 . .
Related
note:
Transformations that preserve the magnitudes of angles but
not necessarily the sense of the angles are called
isogonal.
1- Theorem
Let w=f(z
)be a transformation. At points where
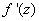 exists and is nonzero, this transformation is conformal
.
exists and is nonzero, this transformation is conformal
.
Proof.
Let z=z(t)
=x(t)+y(t), a≤t≤b represent an arc C.
Thus the
slope of the curve is
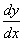 .
So at any point where z .
So at any point where z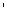 (t)≠0,
z (t)≠0,
z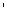 (t)
is tangent to C and arg z (t)
is tangent to C and arg z
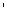 (t)
measures the angle that the tangent makes with the
x-axis. Now (t)
measures the angle that the tangent makes with the
x-axis. Now
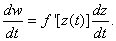
Suppose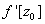 ≠
0, ≠
0,
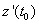 ≠0.
Then w ≠0.
Then w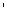 ( (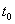 )≠0
and )≠0
and
arg w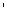 ( (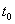 )=arg
f )=arg
f
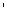 ( (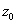 )+arg
z )+arg
z
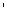 ( (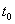 ).
That is, ).
That is,
arg f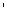 ( (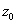 )=
arg w )=
arg w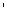 ( (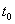 )-arg
z )-arg
z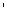 ( (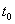 ) )
which is
the angle between the directed tangent to C at 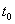 and the directed tangent to the image of C at the
image of
and the directed tangent to the image of C at the
image of
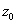 .
In other words, the directed tangent to any arc through .
In other words, the directed tangent to any arc through
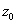 is rotated by an angle arg f
is rotated by an angle arg f
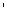 ( (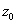 )
that is independent of the choice of arg z ( )
that is independent of the choice of arg z (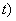 through through
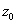 .
In particular, if two arcs intersect at .
In particular, if two arcs intersect at
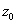 ,
the angle of intersection –in magnitude and sense- is
preserved by the transformation and so this transformation
is conformal. ,
the angle of intersection –in magnitude and sense- is
preserved by the transformation and so this transformation
is conformal.
2-
General
equations of particular transformations
2.1
Translation
w=z+a
where a is a complex constant.
2.2
Rotation
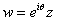 where where
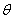 is an angle. If
is an angle. If
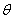 >0,
the rotation is in the counter-clockwise direction and if >0,
the rotation is in the counter-clockwise direction and if
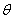 <0,
the rotation is in the clockwise direction. <0,
the rotation is in the clockwise direction.
2.3
Stretching
and contraction
w=az
where a is a positive number. If a>1, the
transformation is stretching while for 0<a<1,
the transformation is a contraction.
2.4
Inversion

2.5
Linear
Transformation
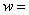 az+ az+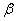 |

