|
Exercise 1.
Let
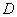 be a domain, symmetric with respect to the real axis,
having a nonempty intersection
be a domain, symmetric with respect to the real axis,
having a nonempty intersection
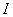 with it. Each holomorphic function in D can be expressed
uniquely in the form
with it. Each holomorphic function in D can be expressed
uniquely in the form
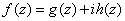 for each
for each
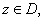 where where
g and h are two
holomorphic functions in
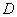 and real on
and real on
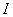 Show that
Show that
 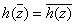 ,
and ,
and
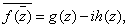 for each
for each
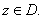
Exercise
2.
Let
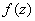 be a non-constant holomorphic function on a domain
be a non-constant holomorphic function on a domain
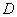 and let
and let
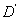 be a domain such that its closure
be a domain such that its closure
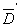 is compact and contained in
is compact and contained in
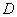 .
Show that, if .
Show that, if
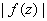 is
constant on the boundary of is
constant on the boundary of
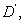 then
there exists at least one zero of then
there exists at least one zero of
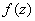 in
in
 (consider (consider
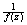 and use a contradiction argument).
and use a contradiction argument).
Exercise
3.
Let
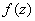 be a holomorphic function in the disk
be a holomorphic function in the disk
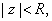 and
put and
put
 for
for
0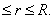 Show that
Show that
a)
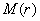 is
a continuous and increasing function of is
a continuous and increasing function of
 in 0
in 0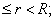
b) If
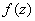 is not constant, then
is not constant, then
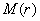 is strictly increasing.
is strictly increasing.
Exercise 4.
Let
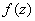 be holomorphic in
be holomorphic in
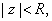 and
put and
put
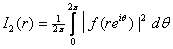 for
for
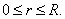
Show that,
if
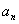 denotes the
denotes the
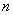 th
Taylor coefficient of th
Taylor coefficient of
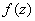 at
at
 then
then
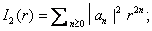
deduce
that, if
 then
then
i)
 is
an increasing continuous function of r; is
an increasing continuous function of r;
ii)
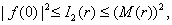
iii)
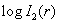 is
a convex function of log is
a convex function of log
 in the case where
in the case where
 is not identically
is not identically
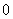 (show that ,if we put
(show that ,if we put
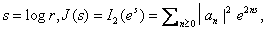
we have
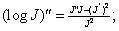 to
show that to
show that
 use the Cauchy-Schwarz inequality on the absolutely
convergent series:
use the Cauchy-Schwarz inequality on the absolutely
convergent series:
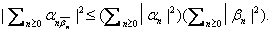
Exercise 5. Let
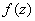 be a holomorphic function on the disk
be a holomorphic function on the disk
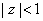 such that
such that
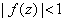 on this disk; if there exist two distinct points
on this disk; if there exist two distinct points
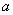 and
and
 in the disk such that
in the disk such that
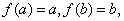 then we must have
then we must have
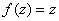 on the disk.
on the disk.
(consider
the function
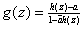 with with
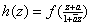 from which we have
from which we have
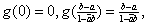 and and
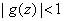 in the disk).
in the disk).
Exercise 6
Hadamardís
theorem on the real part: Let
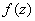 be a holomorphic function in an open set containing the
disk
be a holomorphic function in an open set containing the
disk
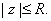 For
For
 put put

i) Show
that
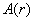 is an increasing continuous function of
is an increasing continuous function of
 (notice that
(notice that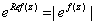 ). ).
ii) If we
have in addition
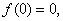 then,
for then,
for
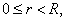 we have
we have
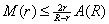
(consider
the function
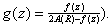
iii) For
 show that
show that
 |

