|
1.
Prove that
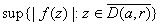 is
attained at a point of is
attained at a point of  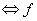 is
constant on is
constant on 
is equivalent
to
 has
a relative maximum at a has
a relative maximum at a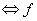 is
constant in a neighborhood of a is
constant in a neighborhood of a
2. Let f(z)
be a non-constant analytic function on the disk 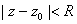 with with
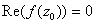 .
Show that on every circle .
Show that on every circle 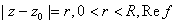 assumes
both positive and negative values. assumes
both positive and negative values.
3. Suppose
that f(z) is an analytic function on a domain D
which contains a simple closed curve 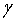 and
the inside of and
the inside of 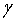 .
If |f| is constant on .
If |f| is constant on 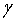 ,
then f is either constant or has a zero inside ,
then f is either constant or has a zero inside 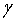 . .
4. Suppose
that f(z) is an analytic function whose modulus |f(z)|
is constant on a domain D. Show that f(z) is
constant.
(Hints:
With 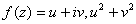 is
constant. Differentiating with respect to x and y we get is
constant. Differentiating with respect to x and y we get 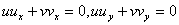 .
Using the Cauchy Riemann equations we get .
Using the Cauchy Riemann equations we get
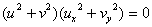 .
If .
If 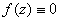 ,
then ,
then  holds
only at individual points, so that holds
only at individual points, so that 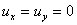 must
hold everywhere and therefore must
hold everywhere and therefore 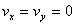 .) .)
5. Let  be
a bounded domain, and consider be
a bounded domain, and consider 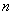 points points 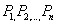 in in 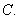 Show
that the product Show
that the product
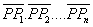 of
distances from a point of
distances from a point  varient
in the closure varient
in the closure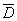 , ,
to the points 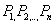 attains
its maximum at a point on the boundary of attains
its maximum at a point on the boundary of 
6.
Three-Circle
Problem of Hadamard:
Let 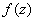 be
a holomorphic function in an open set containing the closed annulus be
a holomorphic function in an open set containing the closed annulus 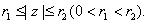 Put Put 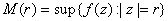 for for 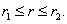
Show that
(1)
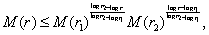
for 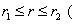 Apply
the maximum principle on the function Apply
the maximum principle on the function 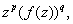 with with 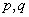 integers
and integers
and 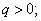 choose
then a real number choose
then a real number 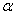 such
that such
that 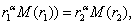 and
a sequence of integers ( and
a sequence of integers (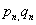 ) )  such
that such
that 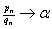 as as
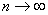 . .
Verify that
inequality (1) implies that 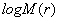 is
a convex function of is
a convex function of 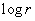 for for
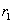 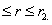
|

