|
Exercise
1.
Solve the equation
a)
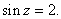
b)
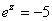 . .
c)
Is the function f(z)=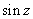 onto? How about f(z)= onto? How about f(z)=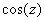 ? ?
d)
Is the function f(z)=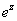 onto? onto?
Exercise 2.
Let
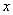 and and
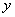 be real
numbers with be real
numbers with
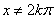  integer integer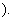 Let Let
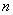 be a
non-negative integer. Show that be a
non-negative integer. Show that
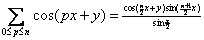
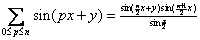
(Use
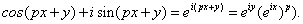
Exercise 3.
Show that
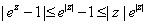 for all for all
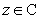
Exercise 4.
Show that
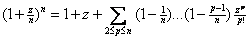 for all
integers for all
integers
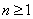 and for all and for all
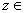 C
and deduce that C
and deduce that
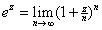 for all for all
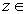 C. C.
Exercise 5.
Show that the function
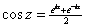 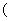 respectively respectively
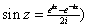 is the
analytic continuation, in is the
analytic continuation, in
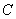 , of the
function , of the
function
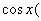 respectively respectively
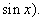
Show that
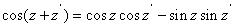
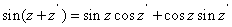
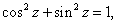
where
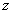 and and
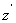 are in
C. are in
C.
Exercise 6.
Show that
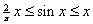 for for
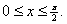
Exercise 7.
Let
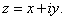
i) Show that
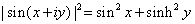
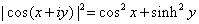
ii) Determine
the zeros of the functions
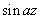 and and
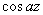 , where , where
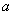 is a non-zero
real number. is a non-zero
real number.
iii) If
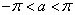 and and
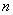 is a positive
integer, show that is a positive
integer, show that
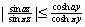 for for
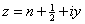
and
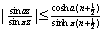 for for
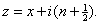
(Hint: Using
definitions,
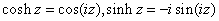 ). ).
Exercise 8.
Let
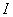 be an
interval in be an
interval in
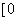 , ,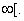 If If
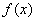 is a
real-valued function with values in
C
which is analytic in I, then we can extend it to an
analytic function in an open and connected subset of
C
containing is a
real-valued function with values in
C
which is analytic in I, then we can extend it to an
analytic function in an open and connected subset of
C
containing
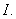
Exercise 9.
i) Let
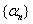 and and
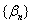 be sequences
s.t. be sequences
s.t.
a) There exists
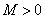 s.t. s.t.
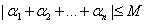 for each for each
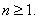
b)
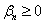 and and
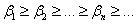
Show that
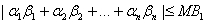 , for each , for each
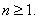
(Introduce
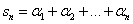 and write and write
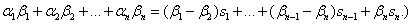
ii) Let
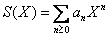 be a power
series with complex coefficients s.t. be a power
series with complex coefficients s.t.
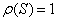 and s.t. and s.t.
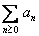 is
convergent. Use (i) to show that is
convergent. Use (i) to show that
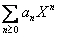 converges
uniformly on converges
uniformly on
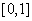 and conclude
that with and conclude
that with
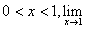 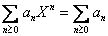 . .
iii) Now let
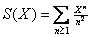 and and
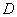 be the
intersection of the disk be the
intersection of the disk
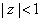 and the disk and the disk
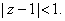 Show that
there exists a constant Show that
there exists a constant
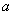 s.t. s.t.
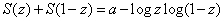 for for
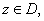 where where
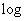 denotes the
principal determination of the complex logarithmic
function defined on the half-plane denotes the
principal determination of the complex logarithmic
function defined on the half-plane
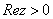 which
contains which
contains
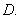
(Note that if
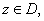 then then
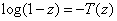 with with
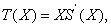 and and
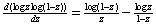 for for
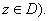
Use (ii) to show
that
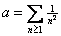
and
 |

