|
Exercise 1.
Prove Greenís Theorem:
Suppose that D is a domain with boundary C both
contained in an open set S on which f has
continuous partial derivatives. Then

Exercise 2.
Let f and g be two holomorphic functions on
a domain
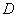 of the plane, not identically zero on of the plane, not identically zero on
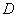 ; if there exists a sequence { ; if there exists a sequence {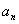 } of points in D such that } of points in D such that
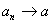 as as
 with with
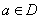 and and
  for all for all
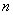 , show that there exists a constant , show that there exists a constant
 such that such that
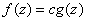 on on
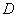
Exercise 3.
Let
 be a continuous function on the
oriented boundary be a continuous function on the
oriented boundary
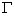 of a compact set of a compact set
 Let Let
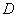 be the open complement of be the open complement of
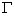 in
C.
For in
C.
For
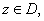 put put
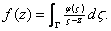
i) Put
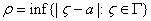 for for
 Show that, for Show that, for
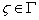 and and
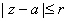 with with
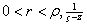 can be expanded as a normally
convergent power series in terms of can be expanded as a normally
convergent power series in terms of
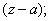 deduce that deduce that
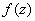 is analytic in a neighborhood of each is analytic in a neighborhood of each

ii) Show that
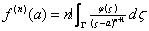 , for all integers , for all integers
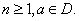
Exercise 4.
Let
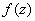 be holomorphic in be holomorphic in
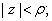 show that if show that if
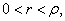 then then
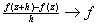 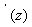 as as
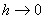 with with
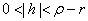 uniformly on uniformly on
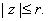
(Hint: Using
exercise 3, write
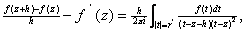 where where
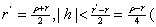 for example for example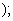 deduce that if deduce that if
 then then
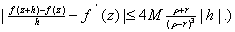
Exercise 5.
Let
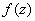 be holomorphic in be holomorphic in
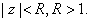 Evaluate, in two different methods,
the integral Evaluate, in two different methods,
the integral
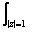 (2 (2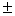 ( (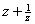 )) ))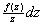
with the unit circle oriented in the direct sense and
deduce the following equalities:
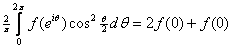

|

