|
1. Our objective here is to deduce Liouvilleís theorem
from Parsevalís identity:
Let
 be
an entire function which is bounded by M. be
an entire function which is bounded by M.
a) Applying Parsevalís identity , show that
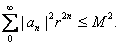
b) Verify that the left-hand side of the inequality in
a) can have no term
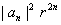 with with
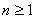 . .
c) Deduce that
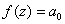 . .
2. Our objective here is to deduce Cauchyís Inequality
from Parsevalís identity:
Without
loss of generality, let
 be analytic in a disk be analytic in a disk
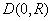 and let and let
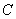 be the circle be the circle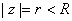 . Suppose . Suppose
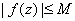 in in
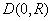 for some positive constant . for some positive constant .
As in problem 1. a)
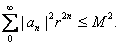
a) Deduce that
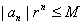 for
every integer for
every integer
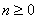 . .
b) Now deduce
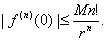
c) Finally deduce Cauchyís Inequality.
3. Our objective here is to deduce the Maximum
Principle from Parsevalís identity:
Suppose
 is an analytic function in is an analytic function in
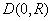 , where the function , where the function
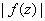 has a
maximum M in has a
maximum M in
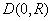 .
We need to show that .
We need to show that
 is
constant. is
constant.
a) Let
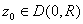 be such that be such that . Then there exists some r
with . Then there exists some r
with
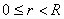 such that such that
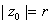 . Applying Parsevalís identity, show
that . Applying Parsevalís identity, show
that
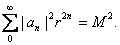
b) Deduce that
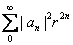 cannot
have any terms except cannot
have any terms except
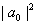 . Thus . Thus
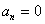 for integers
for integers
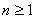 .
Consequently, .
Consequently,
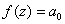 . .
4. Our objective here is to give another proof of
Liouvilleís theorem by using Cauchyís formula:
Let
 be an entire function which is bounded by M.
Let be an entire function which is bounded by M.
Let
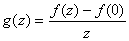 . .
a) Show that
 is an entire function. is an entire function.
b) Show that, for
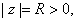 we have we have
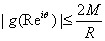 . .
c) Let w be a point and suppose R is
large enough so that
 . Using Cauchyís formula, show
that . Using Cauchyís formula, show
that
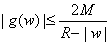 . .
d) Deduce that
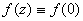 . .
|

