|
In this
session we consider the transformation
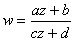 where a,b,c,d are complex constants satisfying
ad-bc≠0.
where a,b,c,d are complex constants satisfying
ad-bc≠0.
This
transformation is clearly a combination of translation,
rotation, stretching or
contraction, and inversion.
This
transformation is called bilinear because it is
equivalent to
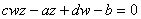 , ,
where the
left-hand side is seen to be linear in z and w.
If we
expect circles to map into circles; that is,
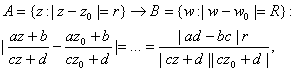
we notice
the “problem” in the variable term |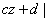 and
we now set our objective to show that this special
conformal transformation maps “lines and circles” into
“lines and circles” in the extended complex plane and
we now set our objective to show that this special
conformal transformation maps “lines and circles” into
“lines and circles” in the extended complex plane
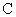 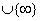 as we shall see shortly. If c=0, then
as we shall see shortly. If c=0, then
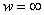 implies
implies
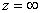 .
If .
If
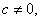 then
then
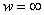 implies that
implies that
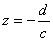 and
and
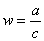 implies that
implies that
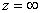 .
Notice that this correspondence is continuous in the sense
that as .
Notice that this correspondence is continuous in the sense
that as
 then
then
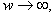 and as
and as
 ,
then ,
then
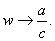 The inverse transformation
The inverse transformation
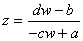 shows a one-to-one correspondence from the extended
complex plane onto the extended complex plane.
shows a one-to-one correspondence from the extended
complex plane onto the extended complex plane.
Theorem. The
equation of any line or circle in the complex plane can be
written in the form
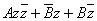 +C=0, +C=0,
where A
and C are real numbers with AC<|B|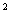
Proof.
For A=0
the equation reduces to
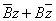 +C=0.
Letting z=x+iy and B= +C=0.
Letting z=x+iy and B=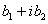 we get (
we get (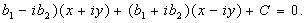 Then Then
 which
represents a line. which
represents a line.
Now the
equation of a circle with center
 and
radius and
radius
 is
is
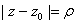 or
or
 .
Thus .
Thus
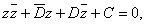 where
where
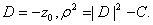
For
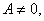 the equation above clearly represents a circle.
the equation above clearly represents a circle.
In the
extended complex plane, lines can regarded as circles
through
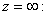
As a
matter of fact, in the case
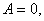 replacing z by
replacing z by
 transforms
the resulting equation into transforms
the resulting equation into
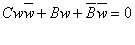
which for
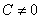 is a circle. Hence we group circles and lines in one
category.
is a circle. Hence we group circles and lines in one
category.
Since
z=w-b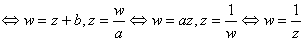 it follows that under these three transformations “lines
and circles” are mapped into “lines and circles”. Now we
show that this is also true for any bilinear
transformation:
it follows that under these three transformations “lines
and circles” are mapped into “lines and circles”. Now we
show that this is also true for any bilinear
transformation:
If
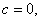 then then
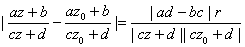 implies that the result is true in this case.
implies that the result is true in this case.
If
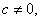 then by dividing the numerator and denominator in the
general bilinear transformation by
then by dividing the numerator and denominator in the
general bilinear transformation by
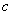 ,
we may write the transformation as ,
we may write the transformation as
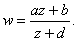 Making the substitution
Making the substitution
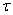 =z+d
yields =z+d
yields
 which can be regarded as an inversion
which can be regarded as an inversion
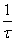 followed by a magnification and rotation
followed by a magnification and rotation
(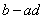 ) )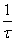 ,
followed by a translation ,
followed by a translation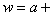
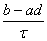 . .
|

