1.
Activity 1
Letís see how Maple can be used to find the residue of the
function
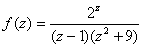 at the pole z=1. at the pole z=1.
>
f:='f': s:='s': z:='z':
f := z -> 2^z/((z-1)*(z^2+9)):
`f(z) ` = f(z);
s := series(f(z), z=1, 5):
`f(z) ` = s;
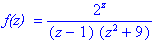
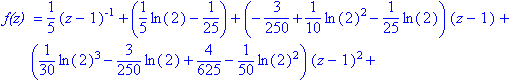
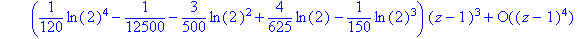
Thus this residue is
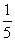 . .
2.
Activity 2
Using the result
of activity 1) , continue using Maple to evaluate
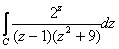 ,
where C is the circle ,
where C is the circle
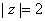 . .
>
f:='f': F:='F': s:='s': z:='z':
f := z -> 2^z/((z-1)*(z^2+9)):
`F(z) ` = f(z);
s := series(f(z), z=infinity, 5):
res := 1/5:
`Res[F,1] ` = res;
print(int(F(z),z=C..``) = `2*Pi*I*Res[f,1])`);
print(int(F(z),z=C..``) = 2*Pi*I*res);
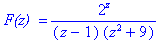
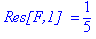
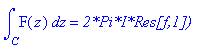
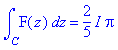
3.
Activity 3
We can have a Cauchy Residue Theorem to integrals that
have a finite number of isolated singularities (not
necessarily poles) that lie inside the contour C.
This example, where the integrand has an essential
singularity, shows how we can use Maple to check the value
of an integral.
>
f:='f': s:='s': z:='z':
f := z -> exp(1/z):
s := series(f(z), z=infinity, 5):
`f(z) ` = f(z);
`f(z) ` = s;
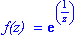
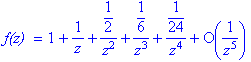
Thus the residue is
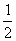 . Now we augment this with an
application of the
Cauchy Residue Theorem. . Now we augment this with an
application of the
Cauchy Residue Theorem.
>
f:='f': F:='F': s:='s': z:='z':
f := z -> exp(1/z):
`F(z) ` = f(z);
s := series(f(z), z=infinity, 5):
res := 2:
`Res[F,0] ` = res;
print(int(F(z),z=C..``) = `2*Pi*I*Res[f,0])`);
print(int(F(z),z=C..``) = 2*Pi*I*res);
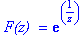
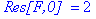
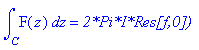
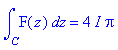
4.
Activity 4
Do
some Maple experimentation with other functions by finding
their residues and integrals. |

