1-
Morera’s Theorem
The following theorem can be considered a converse of
Cauchy’s Theorem and is often useful in proving that a
function is analytic:
Theorem (Morera).
Suppose
that f(z) is continuous in a domain D and
 for every triangle T which together with its
interior lie in D. Then f(z) is analytic in
D. for every triangle T which together with its
interior lie in D. Then f(z) is analytic in
D.
To prove Morera’s Theorem we use the following lemma whose
proof is a slight modification of the proof of Cauchy’s
Theorem:
Lemma.
Suppose
that f(z) is continuous in a star domain D
and
 for every triangle T which together with its
interior lie in D. Then there exists a function
F(z) analytic in D such that F’(z)=f(z). for every triangle T which together with its
interior lie in D. Then there exists a function
F(z) analytic in D such that F’(z)=f(z).
Proof of Morera’s Theorem. Let
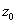 be any point in D.
Choose a positive number
r small enough so that the disk be any point in D.
Choose a positive number
r small enough so that the disk
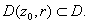 Thus the star
domain Thus the star
domain
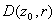 satisfies the hypothesis of the lemma and so there
is an analytic function F(z) such that F’(z)=f(z)
in satisfies the hypothesis of the lemma and so there
is an analytic function F(z) such that F’(z)=f(z)
in
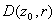 . Since
F(z) is analytic in . Since
F(z) is analytic in
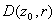 it has
analytic derivatives of all orders in it has
analytic derivatives of all orders in
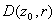 and, in
particular, F’(z)=f(z) is analytic in and, in
particular, F’(z)=f(z) is analytic in
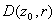 . But . But
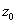 was an arbitrary point in D.
Consequently, f(z)
is analytic in D. was an arbitrary point in D.
Consequently, f(z)
is analytic in D.
Corollary. Suppose
that f(z) is continuous in a domain D and analytic
at all points of D except possibly at the points of
some line
 . Then f(z) is analytic on
D. . Then f(z) is analytic on
D.
Proof. Rotating if necessary, we may assume that
 is parallel to
the x-axis. Now the result follows from Morera’s
Theorem. is parallel to
the x-axis. Now the result follows from Morera’s
Theorem.
2- Analytic Continuation Principle
We state without proof the following useful:
Theorem (Analytic Continuation Principle). If two analytic functions f and g agree in a
neighborhood of a point of a domain D, then they
agree on D.
3- Reflection Principle
Theorem. Let
D be a domain of
C
symmetric with respect to the real axis. Let
 , ,
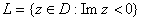 ,
and ,
and
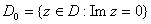 . .
Let g(z) be continuous on
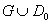 , holomorphic on
G and , holomorphic on
G and
 R.
Then there is a unique function R.
Then there is a unique function
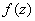 holomorphic on D
such that its restriction to holomorphic on D
such that its restriction to
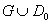 is g(z). is g(z).
Proof. Consider the function h(z) defined on
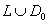 by
by
 . Since the function . Since the function
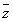 is continuous, h(z)
is continuous on is continuous, h(z)
is continuous on
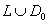 . We now prove that
h(z)
is holomorphic on L by proving that it is
holomorphic at each . We now prove that
h(z)
is holomorphic on L by proving that it is
holomorphic at each
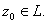 Now Now
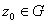 . Since g(z) is
holomorphic on G, it is analytic there and so there
exists r>0 such that . Since g(z) is
holomorphic on G, it is analytic there and so there
exists r>0 such that
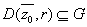 and and
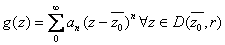 .
Now for all .
Now for all
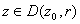 we
have we
have
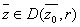 .
So by a limiting process we get .
So by a limiting process we get
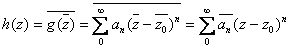 and therefore h(z) is analytic on L
and hence holomorphic there. Consider the function and therefore h(z) is analytic on L
and hence holomorphic there. Consider the function
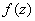 on
D defined by on
D defined by
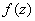 = g(z) if = g(z) if
 and h(z) if and h(z) if
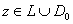 . By
hypothesis, g(z) is real on . By
hypothesis, g(z) is real on
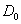 . Thus . Thus
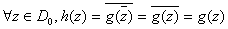 . So . So
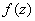 is continuous on D and holomorphic on D
except possibly on is continuous on D and holomorphic on D
except possibly on
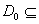 R.
Thus, R.
Thus,
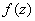 is holomorphic on D by the previous
corollary. Clearly, is holomorphic on D by the previous
corollary. Clearly,
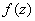 extends g(z) and extends g(z) and
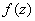 is
unique by the Analytic Continuation Principle. is
unique by the Analytic Continuation Principle.
Example. Suppose that f(z) is an entire function that is
real-valued on an interval (a,b) of the real axis.
Put
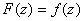 if if
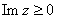 and and
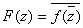 if if
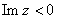 . By the reflection principle F(z)
is analytic on the union D of the upper and lower
semi-planes and (a,b). Moreover, f(z) is
analytic on D and agrees with F(z)
for . By the reflection principle F(z)
is analytic on the union D of the upper and lower
semi-planes and (a,b). Moreover, f(z) is
analytic on D and agrees with F(z)
for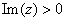 . Thus, . Thus,
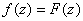 on D.
In particular, on D.
In particular,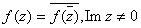 . Furthermore,
f(z) is continuous on
C
. Consequently, for any . Furthermore,
f(z) is continuous on
C
. Consequently, for any
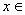 R, R,
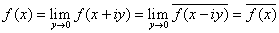
and therefore f(z) is real on the real axis. |

