RESIDUE
SHORTCUTS WITH EXAMPLES
We now mention
some shortcuts that can sometimes be used to speed up the
calculation of residues:
If
 has a pole of order
has a pole of order
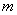 at
at
 ,
then ,
then
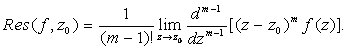
Letís justify
this rule. The Laurent series of f corresponding
to a pole
of order
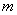 at
at
 is is
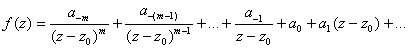
So
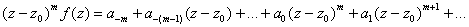
Differentiating
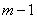 times
yields times
yields
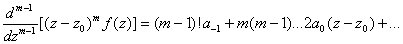
Letting
 gives the result.
gives the result.
As a particular
case we have
If
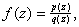 where
where
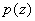 and
and
 are analytic at
are analytic at
 ,
has a simple pole at ,
has a simple pole at
 ,
then ,
then
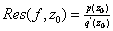 (Notice that
(Notice that
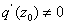 since
since
 is a simple zero of
is a simple zero of
 ).
Indeed, from above with m=1 have ).
Indeed, from above with m=1 have
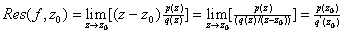 . . |

