|
Definition.
The exponential function,
denoted by 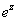 , is defined by , is defined by
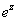 = =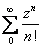
Proposition.
1)
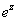 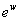 = =
2)
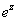 ≠0 ≠0
3)
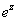 is differentiable on
C
and ( is differentiable on
C
and (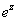 )′= )′=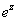
4) The
restriction 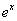 of of
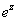 to
R
is a positive strictly increasing function such that to
R
is a positive strictly increasing function such that
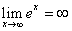 and and
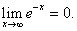
5) There
exists a positive number
p
such that 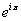 =0. The function =0. The function
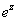 is periodic with periodic 2pi. is periodic with periodic 2pi.
6) 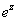 =1 if and only if there is a k
in
Z
such that z=2pki. =1 if and only if there is a k
in
Z
such that z=2pki.
7) Let
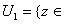 C:
|z|=1}. The mapping C:
|z|=1}. The mapping
 from
R
to from
R
to 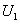 is indeed onto. is indeed onto.
8) For
every nonzero complex number w, there exists z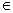 C
such that w= C
such that w=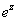 . .
Proof.
1)
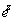 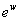 = =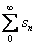 where where
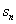 = =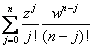 = =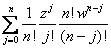 = =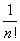 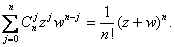
Thus
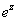 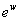 = =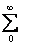 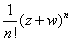 = = . .
2)
By 1) 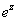 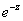 = =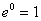 . So . So
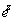 ≠0. ≠0.
3)
(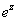 )′=( )′=(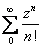 )′= )′=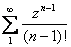 = =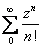 = =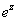 . .
4)
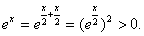 In
addition,
since In
addition,
since 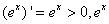 is strictly increasing on
R.
Moreover, is strictly increasing on
R.
Moreover, 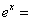  for
x>0
and
so for
x>0
and
so 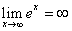 . .
Furthermore, 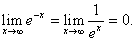
5)
Let
 R.
For all R.
For all  C, C,
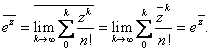 In particular, In particular,
 and
so and
so 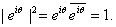 So So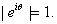 Let Let
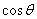 and and
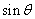 denote denote
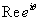 and and
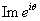 respectively. Then respectively. Then
 and thus and thus
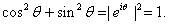 Moreover, Moreover,
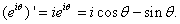 Thus Thus
 It follows that It follows that
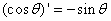 and and
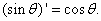
Now
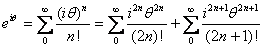 since each series is convergent. since each series is convergent.
That is,
 . .
It follows
that 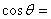 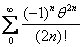 and and
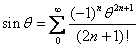 . .
In
particular, 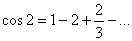
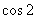 is an alternating series whose general
term decreases in modulus to 0. So is an alternating series whose general
term decreases in modulus to 0. So
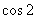  But But
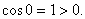 So 0Î[ So 0Î[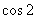 , ,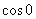 ] and therefore , by the Intermediate
Value Theorem, there exists at least one ] and therefore , by the Intermediate
Value Theorem, there exists at least one
 such that such that
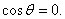 Let Let
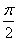 be the smallest be the smallest
 such that such that
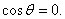 Then Then
 and and
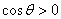 for all for all
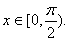 Since Since
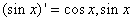 is increasing in is increasing in
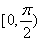 . So for all . So for all
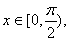 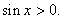 In particular, In particular,
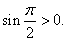 Thus, since Thus, since
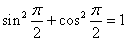 , ,
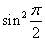 =1. That is, =1. That is,
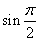 =1 since =1 since
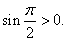 Now Now

Finally,
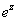 is periodic with period is periodic with period
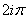 since since
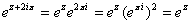
and
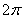 is the smallest positive number p
with the property is the smallest positive number p
with the property
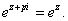
6)
(Ü)
If 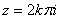 for some integer k, then for some integer k, then
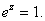
(Þ)
Suppose 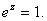 Then Then
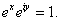 So So
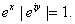 Thus Thus
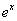 =1 and so x=0. It follows that
z=iy. We need to show that iy=2kpi
or =1 and so x=0. It follows that
z=iy. We need to show that iy=2kpi
or 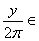 Z.
By the periodicity of Z.
By the periodicity of
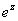 , it is enough to consider , it is enough to consider
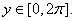 Suppose, to get a contradiction, that Suppose, to get a contradiction, that
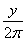 Ï
Z.
Then Ï
Z.
Then  Put Put
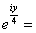 a+ib so that a= a+ib so that a=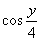 and b= and b=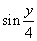 since since
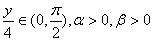 . Now . Now expanding 1= expanding 1=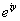 in terms of a and b leads to a
contradiction. in terms of a and b leads to a
contradiction.
7) Let
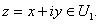 There are four cases to consider
depending on the four quadrants that z may lie in. There are four cases to consider
depending on the four quadrants that z may lie in.
Case 1.
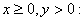 Here Here
 that is, that is,
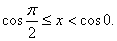 Using the Using the
Intermediate Value
Theorem there is
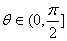 such that such that
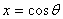 so so
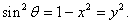 Here Here
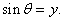 This implies that This implies that
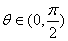 and and

Case 2.
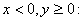 Here Here
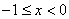 and and
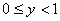 . Then . Then
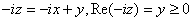 and and
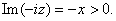 By case 1 there is By case 1 there is
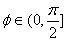 such that such that
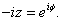 So So
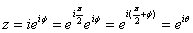 with with
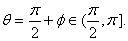
Case 3.
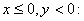 We have We have
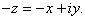 Thus Thus
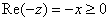 and and
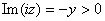 . By case 1 the result follows. . By case 1 the result follows.
Case 4.
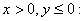 We have We have
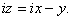 Thus Thus
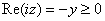 and and
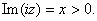 By case 1 the result follows. By case 1 the result follows.
8)
Let
w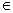 C
-{0}. Put q= C
-{0}. Put q=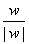 . Then . Then
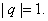 By 6) there exists y By 6) there exists y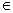 R
such that q= R
such that q=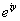 . So w= . So w=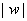 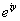 with with
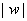 >0. So there exists x >0. So there exists x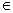 R
such that R
such that 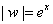 . Therefore, . Therefore,
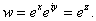
Definitions.
We have just seen that the
mapping  from
R
to from
R
to
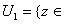 C:
|z|=1} is onto. Thus given C:
|z|=1} is onto. Thus given
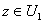 , the set , the set
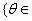 R: R: is nonempty. Each element of this
subset of the real line is called an argument of z
and is denoted by arg z. is nonempty. Each element of this
subset of the real line is called an argument of z
and is denoted by arg z.
The value
of arg z in [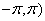 is called the Principal
Determination of arg z
and is
denoted by Arg z. is called the Principal
Determination of arg z
and is
denoted by Arg z.
The
logarithmic Function
We have
seen that the function
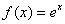 is a strictly increasing function from
R
onto (0, is a strictly increasing function from
R
onto (0, . Thus it has an inverse, denoted by . Thus it has an inverse, denoted by

  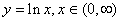 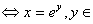 R. R.
Now let
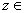 C
- {0}. We have seen that there exists w C
- {0}. We have seen that there exists w
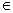 C
such that C
such that 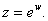 Let Let
w=x+iy.
Then
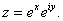 So So
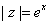 . Thus . Thus
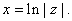 Moreover, Moreover,
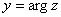 . .
Definitions.
The logarithmic
function,
denoted by
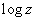 , is defined by , is defined by
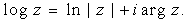
Now the function
 is called the Principal
determination or principal branch of logz. is called the Principal
determination or principal branch of logz.
Definitions. Euler’s equation
 suggests the following definitions suggests the following definitions
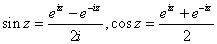 . .
Since
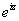 and and
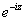 are entire functions, so are are entire functions, so are
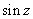 and and
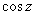 . Using the definition, we see that
most of the real-variable properties hold for complex
variables like . Using the definition, we see that
most of the real-variable properties hold for complex
variables like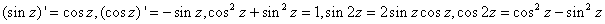 . However, not all real-variable
properties hold as the next example shows: . However, not all real-variable
properties hold as the next example shows:
Example.
Solve
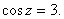
Using the
definition we have
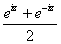 =3. Let =3. Let
 . Then . Then
  or or
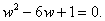 Then Then
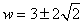 . Consequently, . Consequently,
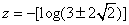 i. i.
Definitions.
As in real
analysis we define the following hyperbolic functions
of a complex variable by
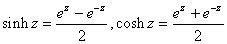 . .
Using the
above definitions it is quite easy to verify that
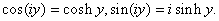
We have
the following results:
Theorem.
1) If
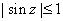 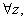 then z must be real. then z must be real.
2)
If 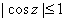 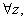 then z must be real. then z must be real.
Proof.
Let
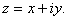 We show that We show that
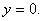

=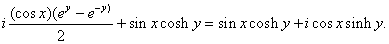
Now
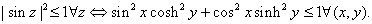
Let
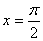 in particular. Then in particular. Then
 But But
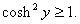 Since Since
 it follows that it follows that
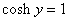 and consequently and consequently
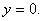
The proof
of 2) is similar where we take
 in particular. in particular. |

