9. CAUCHY’S THEORY
9.1 Cauchy’s Theorem for a Triangle
Theorem 1.
(Cauchy’s theorem for a triangle). Let
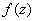 be analytic in a domain be analytic in a domain
 and let and let
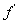 be continuous on be continuous on
 If C is a triangle in If C is a triangle in
 , then , then

Proof.
By Green’s Theorem (exercise 1):
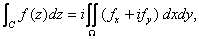
where
 is the inside of the triangle C is the inside of the triangle C
Put
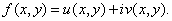 Since Since
 is analytic on is analytic on
 , ,
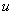 and and
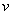 satisfy the satisfy the
Cauchy-Riemann
equations and thus

Remarks.
Indeed, the hypothesis that
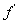 is continuous on is continuous on
 is not needed and there are other
technical proofs. The hypotheses in Green’s Theorem are
satisfied under the assumption that is not needed and there are other
technical proofs. The hypotheses in Green’s Theorem are
satisfied under the assumption that
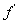 is continuous on is continuous on

9.2 Cauchy’s Theorem for a
star-like domain
Theorem 2.
(Cauchy’s theorem). If
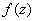 is analytic in a star-like domain is analytic in a star-like domain
 and is a closed contour in and is a closed contour in
 , then , then

Proof.
Since
 is a star-like domain, there is is a star-like domain, there is
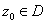 such that the segment between such that the segment between
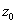 and and
 is in is in
 for each for each
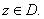 Define Define
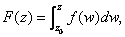 where the path of integration is that
segment. Let where the path of integration is that
segment. Let
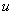 be a point in be a point in
 off this line segment. off this line segment.
By continuity of
 at at
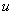 , given , given
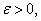 we choose we choose
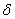 small enough so that small enough so that

Now let
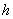 be small enough and satisfying be small enough and satisfying
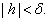 Consider the triangle with vertices Consider the triangle with vertices
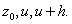 Then, by Cauchy’s Theorem for a
triangle, Then, by Cauchy’s Theorem for a
triangle,

Hence
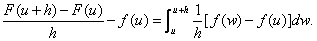
Then
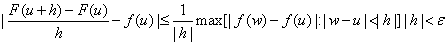
It follows that
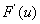 exists and is equal to exists and is equal to
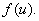
Now with
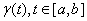 denoting C we have denoting C we have
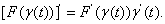
Thus

since C is closed.
9.3 Cauchy’s Integral Theorem
Theorem 3.
(Cauchy’s Integral Theorem). Let
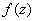 be analytic in a disk be analytic in a disk
 and C is the circle and C is the circle
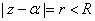 . Then for every . Then for every
 in the disk in the disk
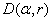 we have we have
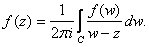
Proof.
Consider the function
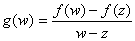 if if
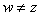 and and
 if if
 . .
Clearly, g is analytic in the star-like domain
 and by hypothesis C is inside and by hypothesis C is inside
 . Thus by Cauchy’s Theorem . Thus by Cauchy’s Theorem
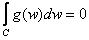 ; that is, ; that is,
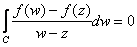 or or
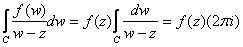 and the result follows. and the result follows.
9.4 Cauchy’s Integral Formula
Theorem 4.
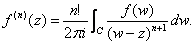
Proof.
Differentiate Cauchy’s Integral Formula n times
with respect to z. |

