|
Exercise 1.
a) Let
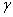 be a piecewise differentiable path and let be a piecewise differentiable path and let
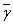 be
its image under the function be
its image under the function
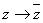 (symmetric with respect to
the real axis). Show that if (symmetric with respect to
the real axis). Show that if
 is a continuous function
on is a continuous function
on
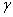 , the function , the function
 is continuous on is continuous on
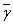 and we
have and we
have
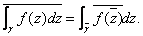
b) In particular, if
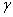 is the unit circle, oriented in
the counter-clockwise direction, then is the unit circle, oriented in
the counter-clockwise direction, then
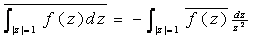
Exercise 2.
Let
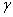 be a continuous path (not necessarily piecewise
differentiable). Show that be a continuous path (not necessarily piecewise
differentiable). Show that
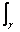 
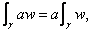
where
 C.
C.
Exercise 3. Let
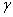 be a piecewise differentiable path whose image is
contained in an open set
be a piecewise differentiable path whose image is
contained in an open set
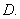
Let
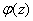 be a holomorphic function on be a holomorphic function on
 with values in an open set with values in an open set
 (in
the plane of the complex variable (in
the plane of the complex variable
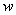 ). Show that ). Show that
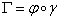 is a
piecewise differentiable path and that for each continuous
function is a
piecewise differentiable path and that for each continuous
function
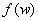 we have we have
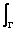 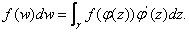
Is this formula
still true in the case where
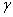 is not differentiable? is not differentiable?
Exercise 4. Let
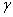 be the (differentiable) path be the (differentiable) path
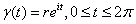 and let
and let
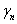 be the path be the path

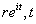 varies in the same interval.
Show that if varies in the same interval.
Show that if
 is continuous in the closed disk is continuous in the closed disk
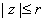 , we have , we have
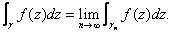
|

